
 |
 |
 |
The database is about RNA Basepairs, their Count, Geometry and Stability. Count: Occurrence frequency in a non redundant dataset of RNA crystal structures obtained from HD RNAs database using the filter of resolution < 3.5 Angstrom and length > 30 nucleotides. Geometry: The orientation of the basepair in 3D space and their interaction pattern. Geometry in crystal context and geometry in ground state optimized structure both are considered here. Stability: Intrinsic stability of different base pairs characterized by interaction energy and its components, which are derived by using Quantum Mechanical (QM) theories. In the subsequent sections we are explaining Geometry and Stability related terms briefly to make the database more interactive. Some terminologies used in the database are widely used but some naming conventions are used in this database for ease of representation. All are explained on this page.
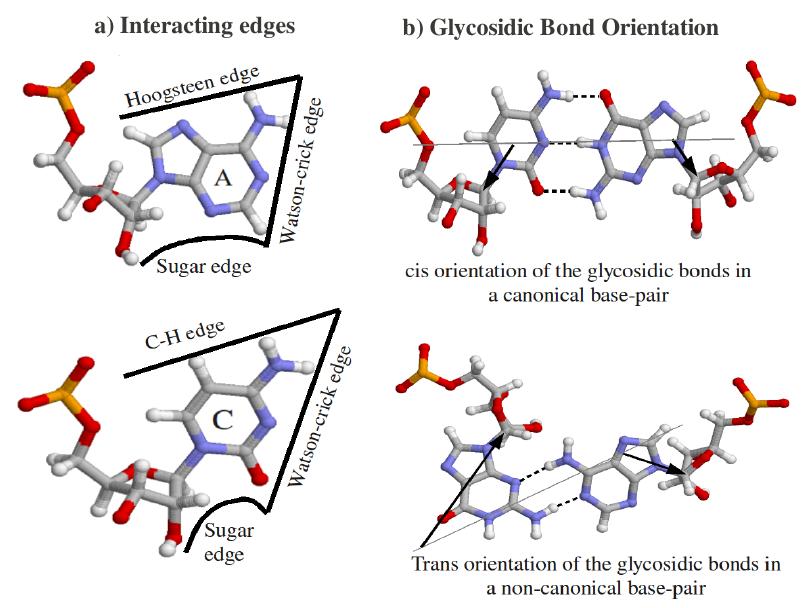
A base pair is characterized by base identities, the interacting edges and respective glycosidic bond orientation of both the participating bases. Based on interacting edges and glycosidic bond orientation Leontis and Westhof Classified base pairs in 12 different classes. Following diagrams explain all possible geometries. Geometric Classification of different Base pairs:
 |
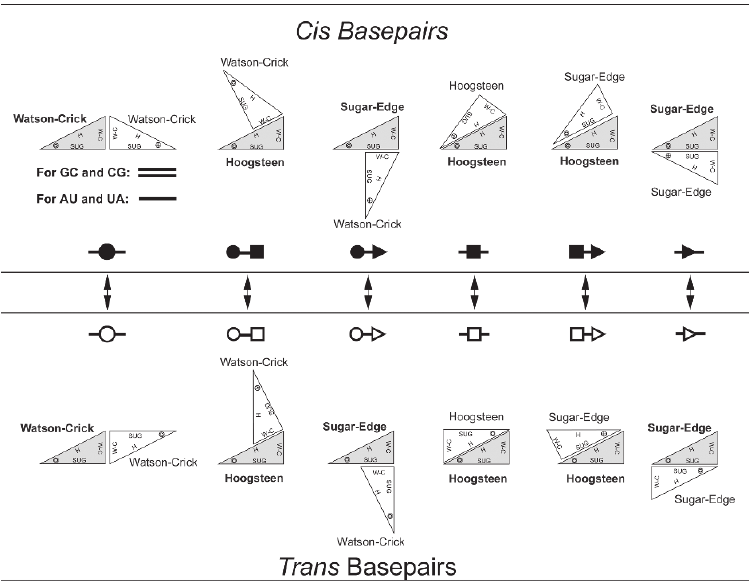 |
RNA molecules consist of 4 different types of nucleic acid bases, and they can interact with each other in 12 different way mentioned above a large number of base pair geometries are possible. Within each geometric family some base pairs are structurally similar, i.e., those can replaced by each other without deviating the overall structure much. Those base pairs are called isosteric base pairs. For each of 12 geometric family, a 4x4 'isostericity matrix' is available which summarizes the geometric relationships between 16 pair wise combinations of the 4 bases in that particular geometric family.
 Reference: N. B. Leontis, J. Stombaugh and E. Westhof, Nucleic Acids Research 2002, 30(16): 3497-3531
Reference: N. B. Leontis, J. Stombaugh and E. Westhof, Nucleic Acids Research 2002, 30(16): 3497-3531
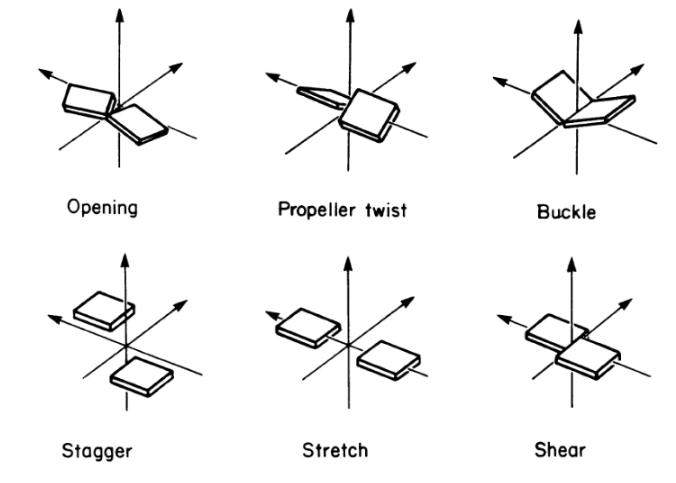
Six different intra base pair parameters describe the orientation of two interacting bases with respect to each other in 3D space. Six parameters are explained by the following figure.To know more Click Here.
E-value is a composite parameter calculated as: E = ∑i (di - 3.0)2 + ½ ∑j (Θj - π)2 (where, di : hydrogen bond heavy atom distance between two bases under consideration , Θj : angle subtended by precursor atoms of both the bases, i : the number of hydrogen bonds that can occur between the two bases, j : the number of pseudo angles for a base pair). Goodness of basepairs increase with decreasing E_values.
Optimization Techniques H_opt: A constrained geometry optimization where coordinates of all the non-hydrogen atoms remain fixed. Full_opt: A geometry optimization with out any constraints on non-hydrogen atoms. Environment Gas Phase: In gas phase calculations, presence of any dielectric medium is not considered, i.e. the system is considered to be in vacuum. Solvent phase (COSMO): In COnductor-like Screening MOdel (COSMO) type solvent phase calculations, the solvent is treated as a continuum with a permittivity ε, and therefore belongs to the 'continuum solvation' group of models. Level of Theory HF: Hartree-Fock (HF) method is an approximation (neglecting electron correlation effect) for the determination of the wave function and the energy of a quantum many-body system in a stationary state. MP2: Møller–Plesset perturbation theory (MP) an improvement over Hartree–Fock method which takes care of electron correlation effects by means of Rayleigh–Schrödinger perturbation theory (RS-PT), to second (MP2) order. RIMP2: It is a 'resolution of identity' (RI) approximation, where the key quantities are expressible in terms of products of single-particle basis functions, which can in turn be expanded in a set of auxiliary basis functions, over MP2 method. B3LYP: Becke, three-parameter, Lee-Yang-Parr (B3LYP) exchange-correlation functional is a hybrid approximation to the exchange-correlation energy functional in density functional theory (DFT) that incorporate a portion of exact exchange from Hartree–Fock theory with exchange and correlation from other empirical sources. PBE0AC: This is another hybrid approximation to the exchange-correlation functional in DFT given by Perdew, Burke and Ernzerhof (PBE0) and is further asymptotically corrected. Basis set Quantum chemical calculations are typically performed using a finite set of basis functions. These functions are combined in linear combinations (generally as part of a quantum chemical calculation) to create molecular orbitals. Some examples are:
Click Here for more details.
Stability of base pairs are characterized by their intrinsic interaction energy calculated by different QM methods. Details of interaction energy calculation in gas phase and solvent phase are described below. Details of calculation of interaction energy in gas phase For the base pairs optimized at M05-2X/6-31G+(d,p) level of theory we calculated the single point interaction energy at MP2/aug-ccpVDZ level. The interaction energy ( ΔEAB) of a base pair AB formed by the individual bases A and B is defined as, ΔEAB = EAB − E0A − E0B where EAB is the total energy of the optimized base pair AB and E0A and E0B are the total energies of the individual bases A and B, in their optimized geometries respectively. This interaction energy was further corrected for Basis Set Superposition Error (BSSE) and deformation energy (Edef(AB)). BSSE correction of the interaction energy (EBSSE ) was done by using standard counterpoise calculations. The deformation energy is represented as, (Edef(AB) ) = (EABA − E0A) + (EABB − E0B) where, EABA and EABB are the energies of the bases A and B respectively in the optimized geometry of AB. So the total corrected interaction energy (Egasint) is calculated as, Egasint = ΔEAB + EBSSE + Edef(AB) Details of calculation of interaction energy in solvent phase Interaction energy of a base pair AB in solvent phase (Esolint) is defined by, Esolint = ΔEsolgas + ΔEcorrection where, ΔEsolgas is the BSSE corrected interaction energy in the gas phase with solvent phase (CPCM) optimized geometries. It is defined by, ΔEsolgas = [EAB – (E0A + E0B)] + EBSSE It is to be noted that, geometry optimization under CPCM paradigm has been done at M05-2X/6-31G+(d,p) level and the interaction energies of the optimized geometries were calculated in MP2/aug-cc-pVDZ level. The energy values associated with the calculation of ΔEsolgas. The second term involved in the calculation of Esolint is a correction term which is defined by, ΔEcorrection = ΔEsol - ΔEgas where, ΔEsol and ΔEgas are the BSSE uncorrected interaction energy values in solvent phase and gas phase respectively, evaluated for the solvent phase optimized geometries. To understand different components of interaction energy, energy decompositions has been carried out by using Kitaura Morokuma scheme or DFT-SAPT methods. The terminology used for different energy parameters are explained below. E_int: Interaction energy E_elec: Electrostatic component of the interaction energy E_ex: Exchange repulsion component of the interaction energy E_pol: Polarization component of the interaction energy E_ct: Charge transfer component of the interaction energy E_hoc: Higher order coupling component of the interaction energy E_ind: Induction component of the interaction energy E_disp: Dispersion component of the interaction energy E_int, E_elec, E_ex, E_pol, E_ct, and E_hoc terms are obtained by using Kitaura Morokuma decomposition scheme with HF/6-31G(d,p) method. E_elec, E_ex, E_ind, and E_disp terms are calculated by using DFT-SAPT energy decomposition scheme with PBE0AC/aug-cc-pVDZ method. For W:S and S:S geometry DFT-SAPT scheme has been used for energy decomposition.
Base-pairs are mainly stabilized by hydrogen bonding interactions, which is a non covalent interactions within an electronegative atom (acceptor) and a hydrogen attached with another electronegative atom (donor). In RNA N-H..O, O-H..O, N-H..N and O-H..N -four types of strong hydrogen bonds and C-H..O and C-H..N- two types of weak hydrogen bonds are possible which stabilize the base-pair. In this database we have reported hydrogen bonding pattern and donor-acceptor distance and angle (based on availability of information). The terminologies used are explained below. DA distance: Distance (in Angstrom) between the Donor and Acceptor atom HA distance: Distance (in Angstrom) between the Hydrogen atom and the Acceptor atiom DHA angle: Angle (in degrees) formed by the Donor atom, Hydrogen atom and Acceptor atom forming the hydrogen bond